当音阶在空间中翻转重叠，几何的结构性和音乐的结构性重合了

蓝狐 10-16 55 抢沙发

默认

摘要： ...

一

微信号：MD80086
添加微信好友, 获取更多信息
复制微信号

YouTube上有个名叫“音乐的几何”的讲座，一位叫作卫斯理（Bill Wesley）的彪悍鬈发大叔跟大家分享他自己发明的键盘乐器。这个后来定名叫“Array mbira”的键盘，把琴键之间的排布重新设计，不再像传统键盘那样从低到高，而是把“和谐”的音放置得尽量近，也就是说，八度音程关系的若干音，一个手指就能弹出来（因为它们分布在一个键的垂直方向，手指“搓动”就可以演奏），然后五度音程的音相邻，为了方便三度、六度等音程，他设置了一些重复的键，这样左右手都可以以小小的移动抵达音符。并且，小调在左手弹，大调在右手弹，这个简单的设计也让一切都变得更方便。这样一来，琴键不是线性的一维，而是平面的二维；弹琴的人即使碰错音，也不会相去太远；更重要的是，转调变得极为容易，因为各个调的键盘看上去都是一样的，不再有黑白键的视觉干扰。他说这样的排布，相当于给乐器增加了一个维度，也就是“情感”，因为和谐度以物理距离的方式呈现了，和谐与否，远近尽收眼底。此外，我想既然西方音乐中有大量的多声部，那么它本来就至少是二维的，有线条，有和谐度，卫斯理的排布不过是用他的方式实现了这个概念而已。

在他的设计中，整个键盘很小，手指的小小移动就能解决大部分的和声进行，甚至能够囊括比较复杂的转调的作品，包括贝多芬著名的转调，都可以清晰地表达出来。因为涉及自己的调律问题，这个综合了几何、算术和物理的设计并不简单，它也不是横空出世，20世纪80年代就有人申请了一种以五度相邻构建键盘的专利（Wicki/Hayden）。这个呵呵憨笑的比尔大叔，在那个视频里自豪地展示他的酷炫乐器。这些看上去只有若干小按钮的键盘，演奏者只需手指轻轻挠拨按压，当真能弹出管风琴那样的效果——从动作表面看，倒真是一种“极简主义”。在我知道的用手演奏的乐器里，恐怕没有谁比他的动作更小。视频是2011年的，至今他们一伙人仍在演奏好玩的炫技音乐，乐器的小家族也在不断扩充，已经包括竖琴了。

我不知道这易上手、声音极为可爱的乐器会不会成为“主流”键盘乐器，能不能登上大雅之堂，至少它的思路很合我口味。我们所习惯的那种从左到右也就是从低到高的键盘排布，本来也出自一种隐喻——声音频率渐高，跟“更加靠右”有什么天然的联系吗？没有。这都是人为的、历史的。那么把一种隐喻换成另一种隐喻，有何不好？“越近越和谐”，比尔打的是“便利”的旗号，其野心可不止于此。他的乐器被一些名乐手使用，还参与了电影音乐，追随者包括“斯汀”（Sting）那样的名组合，他希望有一天可以批量生产这种乐器，甚至能改变音乐世界。当然，各种以“和谐度”为距离构建的键盘，还是要面对一个“不和谐怎么搞”的问题。音乐中的不和谐本来是极为重要的部分。不错，在八度、五度这样的声音里，人脑深感愉悦，但不会满足于此。所以，在和谐和不和谐之间漫步，兼顾平衡与立体，是真正的难事，比尔他们也未必做到了。我慕名去听了能找到的“Array mbira”音乐，虽然极易亲近，也很有冲击力，但深度有限——但这也可能是众人还未习惯它，为它写出多种音乐之故。比尔大叔其人，是个爱钻研的科学爱好者（略带民科色彩）和“文艺愤老”，经常在网站上抱怨音乐越来越自动化、越来越贫乏。“我的乐器视频没有那些好玩的小猫照片，我知道不会有人喜欢。”

时至今日，网络让各种传播都成为可能，我经常在YouTube上看见爱好者们设计的各种奇巧乐器，不少人既是音乐爱好者，也是科学爱好者、“思考爱好者”。其实，用“和谐度”这样更有音乐意义的方式来设计键盘，本应是一种相当自然的思路。音乐中的情绪很鲜明，就算被文化加工得很严重，不少人还是有相当的共同感受，这样一来，用标准化的方式来计量和生产音乐中的感情，就极有诱惑力，这种尝试差不多跟音乐有着一样长的历史。古希腊的毕达哥拉斯发现了弦长与音高的关系，继而从这些比例中看出“和谐”的要义，自此之后，作曲家、音乐理论家、数学家和物理学家们，不知想出多少种体系，想把音乐这种看不见摸不着的东西“绳之以法”。也因为它不能乖乖地摁在纸上，所以有许许多多角度去投射它。

18世纪下半叶以降，欧洲的数学有了巨大的发展，音乐则处在一个多种风格涌动的局面，法国和意大利风格，古代风格和“现代”风格（比如法国理论家和作曲家拉莫为代表）共存。这个时期，热爱音乐并从中获得研究方向的数学家和科学家不止一位，比如瑞士数学巨匠欧拉。本来，音乐只是消遣，不过数学本能让他在音乐中也开始思考数学。从十几岁的时候，他就发表了关于“声音传播”的论文，此后几十年都经常回到对音乐的思考中。1730年（当时欧拉23岁），他的想法是“量化”音乐激发的感觉，也就是，通过分析声音的数学和物理特质，计算出“音乐的悦耳度”。当时另一位瑞士数学家，欧拉当时的老师和朋友伯努利对音乐也有兴趣，但在跟欧拉的通信中，他表示这种快感是基础性的东西，不可能量化，可是欧拉并不放弃。

当时，人们已经知道音程中的八度、五度、四度最令人愉悦，三度、六度算是不和谐，又因为音符有周期性（只有七个音符，然后重复），那么用数字来分析它应该是可行的。欧拉把任意的音程按比例标记出来，比如一个三和弦，用p∶q∶r（都是质数）来表示，然后创造出一个“和谐度”或者“悦耳度”（agreeableness，拉丁名“gradus suavitatis”）=p+q+r-2来记录和弦或者音程的和谐程度。这个结果不仅能解释许多（但并非全部）当时对声音和谐程度的认识，而且它跟后代出现的声波叠加的分析是大体一致的。乘积转换成加法的对数工具并非欧拉所发明，但他是第一个用对数来计算音程的人。欧拉的许多想法受当时的文化影响，今人会觉得荒谬，比如把不和谐音程归为“上帝不喜欢不完美数字”，把文化差异解释为“野蛮人欣赏不了我们的音乐，因为他们理解不了我们的音乐中的深刻和谐”等，这些认知，都在社会和文化的变革中被人摒弃了。而在这个探索音乐的过程中，欧拉收获了很多数学思想和工具，比如自然对数（e正是以欧拉命名的）。感谢《音乐与现代科学》（Music and the Making of Modern Science，by Peter Pesic，2014）一书，为我们指出著名的欧拉公式F+V-E=2，［1］和那个并不太成功的音乐公式p+q+r-2，尽管二者应用于完全不同的领域，但有着奇妙的内在联系。之后，欧拉的特性数，X=V+F-E中的X，也被称为“度数”。

不出伯努利所料，欧拉用数字来表达“音乐的快乐和悲伤程度”的“音乐情感公式”，最终留在了他的早期论文里，只供科学史家来爬梳。渐渐地，欧拉在各种新音乐中扩大了自己对音乐“和谐度”的认识。三十年来，欧拉都没忘记音乐对数学的启发。

时至今日，情感仍然是一种“算不清”的东西，当人们企图去计算“快乐”和“悲伤”的数值的时候，这些情绪仍会不断遁形，逃脱各种语言（包括数字）的追索。这是不是人类的宿命？大脑进化至今，仍然是“远古大脑”，仍然残余无法被“升级”的部分，科技也好语言也好，撞在肉身之墙上仍然喏喏退却。语言和情绪的脱节，感性与理性的分离，生理基础相对于社会巨变显出的滞后，仍然源源不断地生产这个人类社会里的各种好戏。

而从另一方面看，音乐难道不是太神奇了吗？音阶中七个音的循环外加一些已知的和声关系，和谐与不和谐的人类感受，竟然给数学和物理打开了这样的天地。追本溯源，这从毕达哥拉斯时代就开始了，比如那个深深困扰人类的，怎么也驯服不了的五度圈。音乐家为这个顾此失彼的调律问题烦恼，科学家帮不上大忙，反倒证明尝试“完美”的调律是白费力气，但人们在这个死角中认识了更深刻丰富的世界。

如今，欧拉的“音乐数学”成就已经被人梳理并出版了相关的著作。他最重要的音乐研究心得却等了一百多年才在音乐理论家那里听到微弱的回响。《音乐新理论的尝试》（TENTAMEN NOVAE THEORIAE MUSICAE EX CERTISSIMIS HARMONIAE PRINCIPIIS DILUCIDE EXPOSITAE）里提出了一个“调性网络”（Tonnetz）：从音程来说，F到C，C到G，G到D都是五度，C到下方A是三度，A到E也是五度。这样一来，十二个音都有了位置，它们不再是一维的性状，而展现了平面关系——不知读者是否像我一样，觉得这个网络跟欧拉著名的七桥图也有几分神似——这些音符也不能遍历。

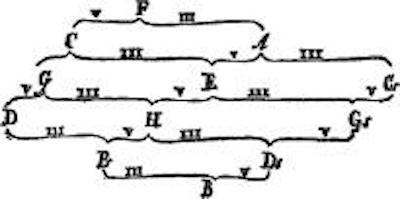
图中字母右边的小s表示升号

注意，欧拉在这里是忽略各个音符的具体音高的，也就是说，某个C音跟高八度的C可视为同一。这样一来，音阶的“扭曲”“粘合”就产生了。音阶不再是直线式，它本身就有了平面结构。

不用说，这跟比尔大叔的键盘有着异曲同工之妙，键盘上琴键的距离可以是我们常见的，按声音频率大体均分的距离，也可以是体现声音同构性的抽象距离。这一切，都来自音符的特性——循环性，以及八度、五度、四度这些深植于生理感知和文化习惯的和谐音程。声音的排列呈现网状之后，音乐理论家们立刻感到音乐的进行可以用图形来表示了。

二

数学家和物理学家则是从另一侧面来想这个问题。著名物理学家亥姆霍兹的诸多成就里，包括声学和神经传导的成果。他追索声音的物理规律，还去钻研人耳的结构，大约是想从“认知”那一端，探索音乐和感觉的奥秘。亥姆霍兹从音乐可以移调而声音相对关系不变这一点出发，指出它的空间性：一个物体在空间中移动，也不会发生改变，这一点和音乐是一样的。也就是说，因为物体在空间中可以移动，音乐中的音高由于有比例性，也就是说，两个音如果距离五度，弦长比是3∶2，如果距离大三度，弦长比是5∶4，那么以此类推，只要保证相对关系不变，音乐就保持不变。那么，音乐一定和“物体运动”具有类似的特质。在这之后，亥姆霍兹持续思考空间问题，在黎曼空间、非欧几何的启示下，将空间、声音、视觉、颜色这些有着诱人联系的课题整理成《论几何原理的起源和意义》（The Origin and Meaning of Geometrical Axioms，1878）等论文。

亥姆霍兹是19世纪的德意志人，此时的文化空气中，音乐兴盛，哲学兴盛，不少科学家都渴望将科学和音乐及艺术统一认识。不过科学帮助人们对声音物理特质的理解迅速提升，音乐家却似乎“听不见”科学的声音。音乐在科学面前沉默，倒是18世纪的欧洲社会剧变，听到了音乐的回答——“古典”的优雅范式消失了，太多的变化破冰而出，曾经对称、收敛的音乐世界再无宁日。无论是莫扎特、贝多芬、舒伯特还是晚一些的肖邦、舒曼、柏辽兹、李斯特、瓦格纳，他们的音乐语言受到文学、绘画甚至政治的影响十分迅速并且可见。而到了19世纪下半叶，数学和物理学明明把声音的传播特质都讲清楚了，却不见任何大作曲家因此再发现一个“特里斯坦和弦”。当时教堂有改革，或者社会有风波的时候，在音乐中引起的变化，远大于揭露物理声音奥秘的傅立叶变换所激发的变化。音乐学家罗森改编美国艺术家纽曼（Barnett Newman）的一句戏言：“音乐学于音乐学家，犹如鸟类学于鸟儿。”科学更是如此。

这时的数学和物理，顶多就是对乐器制造和调律帮了些忙——还不一定是什么大忙，制琴者凭耳朵已经把调律试得差不多，能够满足精度有限又受文化左右的人耳需求，基于无理数计算的“十二平均律”的钢琴调律也就是增加了一种可能性而已。之前的巴赫，虽然被今人认为作曲风格“数学般精确严密”，他受的数学教育偏偏极为贫乏，他甚至没怎么受当时启蒙运动的影响，也没有多少历史证据表明，巴赫了解当时的科学成就。而所谓巴赫音乐的“数学性”，无非是“数字性”、结构性和比例性而已，并未超出小范围内自然数的计算。能在音乐性中兼顾数字，已经相当罕见（也并不孤立，巴托克等作曲家也喜欢让音乐和数字“互文”），更何况它并不是音乐的主要目的。说到比例，有人可能会举出“黄金分割”在艺术包括音乐中应用甚广，这在某种程度上是事实，但不少流行的例子是错误或者夸大的，它其实没那么神奇，此为他话。

这样看来，虽然技术的进步让音乐家们受益，又能通过改变音乐的传播来影响音乐，但科学似乎再也没能伸手直接触及和推动音乐的创作。直到20世纪前，音乐家在其中只是科技成就中被影响的一分子，而不是主动采撷科学思想的人。

就像任何有历史、有一定复杂度的事物一样，科学和音乐，在历史上有一定的遇合，更多的时候还是各说各话。在我们所知的18、19世纪传世音乐家里，几乎无人拥有像样的数学或科学训练（俄国人鲍罗丁例外，不过他的化学家生涯跟作曲事业似乎并无直接正向关联）。科学的逐渐专门化，也令圈外人不能轻易涉足，歌德那样的通才越来越少。

那么，如果“科学只能间接地影响音乐”是个真命题并且是个“问题”的话，它出在音乐家身上，还是音乐身上？原因有很多。泛泛而言，古今中外的艺术家，往往不同程度地拒斥科学。这也可以理解。难道艺术不是承担科学所“余”的部分吗？此外，专门化的科学和专门化的音乐，注定无法在人脑中获得精确的对应，因为不可能那么巧。科学方法、理性思维在任何成体系的分支里都有应用，音乐也不例外，但更抽象复杂的科学原理并不能激发更深刻的音乐。人脑虽能对音乐的“长度”“比例”有所感知，但不大可能精细到科学所抵达的程度；即便感知比例，往往也不是复杂的比例，比如两个音的频率比，但凡悦耳之音往往分母较小（基本在10以内），而不大可能是113/199这样的数字；那些直接依照技术原理或者数学模型的作曲，都不一定影响到音乐品质本身。

你也可以说这并不是问题。数学或物理，是以事物一般性为目标，那么从其他领域（音乐是其中之一）获取结构上的启发，并推广出新法则，是完全可以想象的事情。而音乐针对的是人的耳朵、人的情感，受众的感官功能是有限的，何必去操心宇宙法则呢？

只是20世纪之后，科技对文化的颠覆更大，加上文化的碎片化，总会有艺术家攫取文化中的一面，据为己有。同时，美术中出现了立体主义、抽象派，时间和空间都成为思想的主题。音乐中的十二音、序列主义等都有了数学元素，电子音乐则终于直接地应用上了技术。而对音乐家来说，科学仍然是可选项，不是必选项。20世纪作曲大师斯特拉文斯基就说过：“我完全不懂‘声音’是怎么回事！”

三

特莫斯科（Dmitri Tymoczko）是普林斯顿大学的作曲教授，也是位理论怪才，他为“空间理论”着迷，写出的音乐论文《和弦中的几何》据说是美国《科学》杂志有史以来发表的第一篇音乐论文。YouTube上，有若干他的讲座，关于“音乐的几何”“音乐的空间”“音乐的形状”等。他出生于1969年，紧随“垮掉的一代”生长，父母是大学教授，又是“嬉皮士”，一家人住在嬉皮公社的大房子里，还种植大麻。小时候，父亲曾因为上街抗议越战而被捕。他在这样的家庭中长大，既喜欢智识，又有一身反骨，当然还有对音乐的痴迷。他从小在钢琴和电吉他上弹着摇滚，其间也学点贝多芬和巴赫，后来幸运地遇到一个老师，“把两个世界捏合在一起”。那时候他数学很好，可是最终选择了音乐——曾经也是那么特立独行的父亲，临终时则要他许诺去耶鲁大学读法律而不是学音乐，他答应了，心里却有自己的小算盘。后来，因为种种原因，科斯莫特想过放弃音乐，去哈佛大学读了四年哲学，不成功，最终又回到音乐，认真思考自己的作曲之路。

然而学院里的严肃音乐，永远在“如何让大家接受”的问题上挣扎。特莫斯科戏言，“这些音乐作曲家都得花钱请人来听”，“作曲家终生在大学里勉强糊口，看人脸色”。前辈告诉他作曲家“让餐桌上有食物”是多么不容易，有些令人尊敬的前辈费尽心机帮人找教职，以求同仁们衣食有靠。另一方面，他又很惊讶音乐世界内部的壁垒，严肃、流行、电子、摇滚，音乐学院的老师跟外面完全不在一个世界中。特莫斯科并不想解决音乐的接受问题，但他想去寻求音乐底层的奥秘，至少尝试去表述它。《音乐中的几何》这本大作，是其多年思考的一个总结，谈的是和声进行的“几何表达法”。简单地说，他设计了一些几何空间，连接其中一些点，形成矢量，看看它们最终形成什么模式，或者，按照传统和声原则在这些空间中旅行，看看能产生什么样的音乐。在他的观察下，格利高里圣咏和一首德彪西前奏曲甚至爵士乐手柯川的音乐显示出惊人的联系。上文说过，用空间来表述和声进行，可以说古已有之（比如欧拉的和声网），但现代音乐为它提供了更有意义和更有意思的材料，更何况群论、集合论、非欧几何、拓扑学这些工具，为之提供了更精准的框架。

在他这里，音乐是实实在在地受一些几何观念指引，尽管这并不是多么复杂的几何，并且和不少音乐理论书籍一样，即便从数学出发，数学也随音乐话题的深入渐渐隐形，取而代之的还是音乐实践和音乐判断。数学观念最多仅仅是一个发端和灵感，一个隐喻的借口。即便如此，他的创造力和洞察力还是让人叹为观止。比如第三章“和弦的几何”中有这样一幅十分经典的图，任何读到此书的人都不可错过：

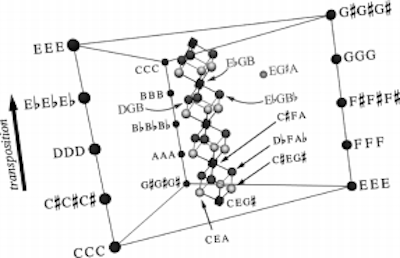
这是个三维空间内表达三和弦（由三个音组成的和弦，比如C—E—G）的图示。我这个普通读者，从他讲二维（三和弦）的时候，就吭哧吭哧用纸来折莫比乌斯环［2］去理解，之后又想象一个棱镜的两端拧了120°对接上，而它的真正模型是只有一个边界，蚂蚁从某点出发会爬回原点的“甜麦圈”。边界上的点是三个相同的音，表面的点是三个音中有两个相同的音。上面这个棱柱图是把甜麦圈掰开重建后的视图，不够直观，不过能显示甜麦圈内部的音。之所以这样扭曲，是基于“不同八度内的同唱名音视为相同”的假设，这也是特莫斯科的出发点之一，他把音符囚禁在一个八度之内，强迫它们折叠，这显然还原不成我们听到的音乐，但音阶在空间之中能够翻转、重叠，恰恰表明为何音乐有无穷可能，却又极为简单。音乐可以漫长、复杂，有曲折的路途，而换一个滤镜去看，比如“和声的距离”，音乐可能极为精练和静止，一剑封喉。

作者用陶土自制的三维空间模型“甜麦圈”，它表达所有三音的组合，不过有些组合在它的内部不可见。它只有一个边界，所有三个音相同的组合都在边界上，两个音相同的组合都在表面。连线表示三音每一步的半音变化。

他写了这本巨著来描述几何模型下的和声进行和对位，自己的作品则践行其理念。让人服气的是，他在经典曲库的数据中挑出一些杰作，来证明有些作曲家在和声进行方面，果真遵循一定的对称原则，符合他的理论，最著名的例子是肖邦的《e小调前奏曲》（Op. 28/4）尽管作曲家是无意识的，尽管他挑选的方式是观念先行的。书中的图示较为烦琐难懂，有人简化成下图：

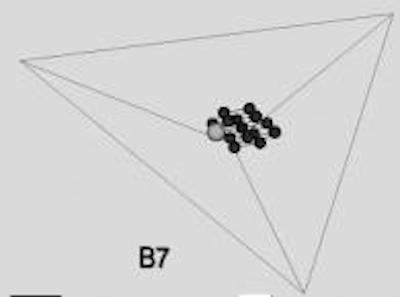
左下角的“B7”是曲子中间的一个和弦，大圆点表示当前的和声，中间一簇圆点表示和弦在空间中的位置。而且，这是一个四维空间的投影。如果读者能看到动图，那会是一场音乐的“星际旅行”。

因为和声进行在他这里用点、线来表示其路径，那么他常常可以指出，某两首作品听上去如此不同，但它们的路径形状相似。这种奇妙的联系让我十分着迷。他认为好听的音乐应该是具有某些几何特质的。不过，在头脑中建立这种联系确实需要漫长的训练，何况特莫斯科对声音的辨别有一个前提：音阶上的音不管八度，只在乎唱名，但一般人的耳朵和大脑并不容易忽视音区。特莫斯科自己或可在脑中建立和弦的几何关系跟音乐的联系，据说数学家欧拉也可以。不过我自己尝试过，至今徒劳。假如，相当多的作曲家接受了这一点，并且将这种“空间听觉”内化成音乐能力，是不是我们的音乐会因此不同？那么所谓音乐如同建筑云云，也真有了另一层极为贴切的意思，甚至可能带来哲学意味的颠覆。自从读了特莫斯科，我虽然不能直接从音乐中“听”出空间，但面对谱面我会多出一些想法，知道音乐的“本质”还有另一重认知可能，音乐是一场运动，一段旅行，但起点和终点，未必是你以为的那样。换句话说，某些音乐体现出一些几何性质，有人把这些性质提取出来，再应用到别的音乐上，发现仍然成立，所以，几何的结构性和音乐的结构性，必然是有所重合的。

四百多页的巨著，涵盖太多“干货”，野心也惊人。作者能在各个门派的前辈杰作中获得印证，尤其是在古典爵士中都能找到这样的统一性，恐怕有种喜大普奔的兴奋。他也承认并不是想把这些和声迁移路线当作作曲秘籍来推销，而只是对一些好的作曲想法给出预测，看是不是会走到死胡同。他还做了个能模仿理论的软件，用鼠标随意选择一些音，它就能显示出和声路径，一切都机械而确定。

我好奇地在互联网上小小研究了一下。原来在空间中用点、线、面来构造和声进行，使音阶翻转、黏合，把线性的音阶编织成网络，也并非前无古人，五花八门的模型一百年来已经有了不少，比如里曼理论、新里曼理论等。“声音的距离”成为实实在在的、可测量的数值，只是它们看上去还是小众的游戏，至于对群论、集合论的应用，跟真正的数学研究比起来，如同过家家，与其说是应用，倒不如说仍然是一种概念性的隐喻。但是，在人工智能拥有无限可能的今天，谁说这些隐秘的联系不能带来真正的改变，甚至人的情绪也能整出傅立叶变换？既然人脸识别都能搞出来，谁说欧拉企图算出“音乐悦耳度”的理想不能实现？

对那一天，我既盼望又略感恐惧。或许我会更留恋人类的浪漫时代，他们天真地以为艺术是可以抵抗科学的，艺术就是抵抗科学的。也有可能，当AI几乎取代一切的时候，科学和艺术又再次分手，因为到了那个时刻，人生还是会剧变的。人脑的进化仍然在吭哧吭哧地缓慢爬行，但人的心智已经不再是这个世界上最强悍的声音。